개발자의 오르막
[코드 트리 챌린지] 유클리드 호제법 본문

개요
글또 블로그를 진행하던 중 코드트리 블로그 챌린지를 참여하게 되는 기회를 얻게 되었다. 코딩 테스트를 집중적으로 준비해보지 않았었기에 항상 코딩 테스트는 부담감이 있는 키워드로 다가왔었다. 이번 기회에서는 코딩테스트에 대한 부담감을 덜고 자신감으로 바뀔 수 있을지 궁금했다.

우선 첫번째 느낌은 일일단위 목표와 진단 히스토리 등 나의 코딩테스트 결과를 끊임없이 알려준다는 것이었다. 파편화된 코딩테스트 문제들을 풀다보면 나의 점수가 정확히 어느정도인지 모르는 경우가 많은데 코드트리에서는 진단히스토리를 메인화면에 보여주고, 주기적으로 업데이트하기를 권장하고 있다.
또한 위처럼 각 난이도별로 문제들을 분류하고, 순서대로 풀기 때문에 스텝 바이 스텝의 형태로 문제를 풀 수 있어 즐거웠다.

깃 계정까지 연동이 가능해서 깃 잔디도 심을 겸 심심풀이로 코딩테스트 문제를 푸는 것이 가능하게 됐다.

제일 인상 깊었던 부분은 글또 챌린지를 위해 대시보드 홈페이지까지 마련해주신 부분이었다. 챌린지를 함께하는 참여자들이 어떤 문제를 풀고, 목표 달성자들은 누구인지 게시해주는 것도 인상 깊었던 부분이었다.
단순히 마케팅만을 필요로 하여 툭 던지는 느낌이 아닌, 챌린지를 함께 하는 사람들이 함께 할 수 있도록 배려해줬던 부분이 인상깊었다.
만약, 코딩테스트를 준비하기 막막한 사람이라면?
반복적인 학습에서 가장 중요한 부분은 반복된 성취감이라고 생각한다. 아무리 바쁘더라도 Low Level 의 코딩 테스트 문제 3개는 무조건 풀 수 있다. (5분정도 걸립니다) 오늘도 3개는 풀고 잔다는 성취감은 코딩테스트에 대한 부담감을 분명하게 덜어준다.
그리고 내가 준비하고자 하는 코딩 테스트 유형별로 분류가 되어있기 때문에 내가 약한 부분을 집중적으로 풀수도 있고, 준비하고자 하는 테스트를 집중적으로도 풀 수 있다. 회사원도 회사원이지만, 취직을 준비하는 취준생의 경우 코딩테스트에 대한 자신감을 분명하게 얻어갈 수 있는 기회라고 생각한다.
우리가 무언가를 부담스러워하고 두려워하는 이유는, 그 무언가가 측정되지 않은 두려움이기 때문이다. 코드트리는 그 두려움을 객관적인 지표를 통해 극복하게 도와준다.
아래는 유클리드 호제법에 대한 내용 정리와 이를 Golang, Java 로 문제를 푼 과정이다.
유클리드 호제법
유클리드 호제법은 두 정수의 최대 공약수(GCD) 를 구하는 방법 중 하나이다.
이 방법은 두 수를 나눠가며 나머지가 0이 될 때까지 반복하여 최대 공약수를 찾는 방법이다.
- a 를 b 로 나누어 떨어지면, b 가 최대 공약수이다.
- a 를 b 로 나누어도 나머지가 있으면 a 를 b 로 나눈 나머지를 새로운 a 로 하고, b 를 이전의 a 로 대체한다.
- 위의 과정을 나머지가 0이 될 때까지 반복한다. 나머지가 0이면 그때의 b 가 최대공약 수이다.
유클리드 호제법 최대공약수 구하는 법
a, b 두 수가 있다면 a, b 를 나누어서 나머지를 r이라고 하면, r 이 0이면 b가 최대 공약수이다.
예시
- GCD(48, 18)
- 48 % 18 = 12
- 18 % 12 = 6
- 12 % 6 = 0
- GCD(54, 12)
- 54 % 12 = 6
- 12 % 6 = 0
- GCD(150, 36)
- 150 % 36 = 6
- 36 % 6 = 0
최소공배수 구하는 법
최소공배수 구하는 방법은 두 수에 대해 곱한 후 최대공약수를 나눠주면 된다.
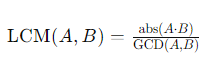
예시
- LCM(150, 36)
- 최대 공약 수 = GCD(150,36) = 6
- 최소 공배 수 = 150 * 36 / 6 = 900
문제풀이 (Golang .ver)
앞서 최대공약수를 구할 때 두 수의 나머지가 0이 될 때까지 계속해서 나누는 것을 알 수 있었다.
특정 조건이 이뤄지기 전까지 로직을 반복할 때에는 재귀함수를 적용 가능하다.
재귀함수의 필요조건
- 동일한 함수를 계속 호출하면서 하나의 함수가 자기 자신을 재귀적으로 호출하게 하는 것
- 재귀가 멈추는 시점
재귀함수
// 유클리드 호제법으로 최대공약수 계산
func gcd(a, b int) int {
if b == 0 {
return a
}
return gcd(b, a%b)
}- 위의 로직은 a%b 의 나머지가 0이 될 때까지 계속해서 gcd 함수를 반복하는 로직이다.
전체 코드
package main
import (
"fmt"
"log"
)
// 유클리드 호제법으로 최대공약수 계산
func gcd(a, b int) int {
if b == 0 {
return a
}
return gcd(b, a%b)
}
// 최소공배수 계산
func lcm(a, b int) int {
return a * b / gcd(a, b)
}
func main() {
var num1, num2 int
// 사용자로부터 두 수 입력 받기
fmt.Print("첫 번째 수를 입력하세요: ")
if _, err := fmt.Scan(&num1); err != nil {
log.Fatalf("정수를 입력해주세요.")
}
fmt.Print("두 번째 수를 입력하세요: ")
if _, err := fmt.Scan(&num2); err != nil {
log.Fatalf("정수를 입력해주세요.")
}
// 최대공약수 계산 및 출력
gcdResult := gcd(num1, num2)
fmt.Printf("두 수의 최대공약수(GCD): %d\\n", gcdResult)
// 최소공배수 계산 및 출력
lcmResult := lcm(num1, num2)
fmt.Printf("두 수의 최소공배수(LCM): %d\\n", lcmResult)
}문제풀이 (Java .ver)
- 앞서 최대공약수를 구할 때 두 수의 나머지가 0이 될 때까지 계속해서 나누는 것을 알 수 있었다.
- 특정 조건이 이뤄지기 전까지 로직을 반복할 때에는 재귀함수를 적용 가능하다.
- 재귀함수의 필요조건
- 동일한 함수를 계속 호출하면서 하나의 함수가 자기 자신을 재귀적으로 호출하게 하는 것
- 재귀가 멈추는 시점
- 두 수를 입력 받아 최대고약수, 최소공배수를 구하는 로직을 구성하였다.
재귀함수
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a%b);
}전체 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
int gcdResult = gcd(a, b);
int lcmResult = (a * b) / gcdResult;
System.out.println(lcmResult);
}
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a%b);
}
}- java 에서도 마찬가지로 gcd 함수를 재귀함수로 구현하였다.
- a 와 b 의 나머지가 0이 안니 경우 b 와 a%b 를 인자로 계속해서 값을 구하였다.
'Algorithm' 카테고리의 다른 글
| 요격 시스템 (ver. golang) (0) | 2024.04.09 |
|---|---|
| [Java] 프로그래머스 레벨2 접두사 문제 (0) | 2019.09.18 |
| 알고리즘 - 선택정렬 (0) | 2019.09.12 |
| [Java] 프로그래머스 레벨1 요일맞추기 (0) | 2019.09.06 |
| [Java]프로그래머스 레벨1 예산문제 (0) | 2019.09.06 |




